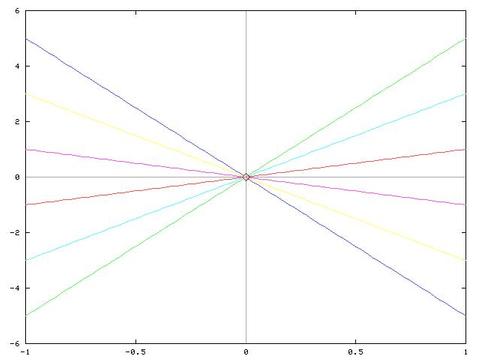
Tilsvarende kan man lægge uendeligt mange parabler (3 parametre) gennem to punkter. Hvis man forsøger at fitte en parabel til følgende datasæt:

-1.0    1.0
 1.0    1.0

giver gnuplot følgende yderst fornuftige besked:

gnuplot> fit f(x) 'etet' via a,b,c
         Number of data points smaller than number of parameters

Med disse to eksempler er det nemt at se problemet. Hvis man derimod har mange data der bare ikke er uafhængige er det sværere. Det man her må gøre er at se på usikkerhedsangivelsen for de enkelte parametre. En stor usikkerhed på bestemmelsen af en parameter indikerer, at der næppe er belæg for at fitte den. Et eksempel på det følger her:

-2.0    3.01
-1.0    0.0
 0.0   -1.01
 1.0    0.0
 2.0    2.99

gnuplot> f(x)=a*x**2 + c
gnuplot> fit f(x) 'data' via a,c

After 1 iterations the fit converged.
final sum of squares of residuals : 0.000251429
rel. change during last iteration : 0

degrees of freedom (ndf) : 3
rms of residuals      (stdfit) = sqrt(WSSR/ndf)      : 0.00915475
variance of residuals (reduced chisquare) = WSSR/ndf : 8.38095e-05

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 1.00143          +/- 0.002447     (0.2443%)
c               = -1.00486         +/- 0.00638      (0.6349%)
 

correlation matrix of the fit parameters:

               a      c
a               1.000
c              -0.767  1.000

gnuplot> plot 'data', f(x)

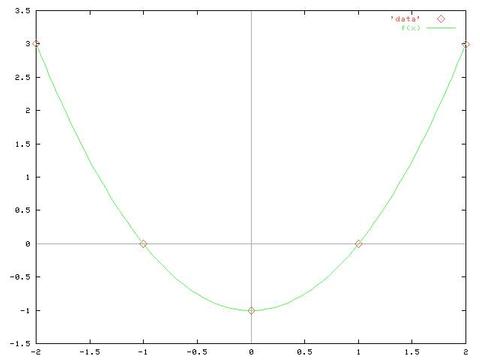
Dette giver et fint fit med små usikkerheder på de fittede parametre. Hvis vi nu bestemmer os for også at have en lineær x-afhængighed i f(x) kommer der problemer fordi denne afhængighed ikke findes i vores data (parabelen er symmetrisk omkring y-aksen):

gnuplot> f(x) = a*x**2 + b*x + c
gnuplot> fit f(x) 'data' via a,b,c

After 1 iterations the fit converged.
final sum of squares of residuals : 9.14286e-05
rel. change during last iteration : -3.88365e-14

degrees of freedom (ndf) : 2
rms of residuals      (stdfit) = sqrt(WSSR/ndf)      : 0.00676123
variance of residuals (reduced chisquare) = WSSR/ndf : 4.57143e-05

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 1.00143          +/- 0.001807     (0.1804%)
b               = -0.004           +/- 0.002138     (53.45%)
c               = -1.00486         +/- 0.004712     (0.4689%)
 

correlation matrix of the fit parameters:

               a      b      c
a               1.000
b               0.000  1.000
c              -0.767 -0.000  1.000

Bemærk at b-leddet er behæftet med en stor usikkerhed og i øvrigt meget småt. Dette udtrykker at der ikke er belæg for b-leddet i dataene, og det mest fornuftige er derfor at udelade det.