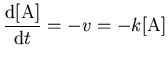
> gnuplot
Programmet starter, og man får en kommandoprompt:
gnuplot>
Man kan nu begynde at skrive kommandoer til gnuplot. Når man vil forlade gnuplot bruger man kommandoen "quit":
gnuplot> quit
Gnuplot kan også køres under windows. Download zip-filen
gp371cyg.zip,
pak den ud i et selvstændigt katalog og kør installationsprogrammet.
gnuplot> plot x**4 - x**2
Man bestemmer hvilket interval der plottes ved at angive først x-intervallet og derefter y-intervallet i kantede parenteser efter "plot". Prøv følgende eksempler:
gnuplot> plot [-1:1] x**4 - x**2
gnuplot> plot [0:3][-1:1] x**4 - x**2
gnuplot> plot [0:3][-1:] x**4 - x**2
gnuplot> plot [0:2*pi] sin(x)
Når man vil plotte data fra en datafil skal gnuplot have lidt flere oplysninger. Først og fremmest skal gnuplot have navnet på datafilen. Vi forestiller os, at vi har en datafil ved navn "testdata" med følgende indhold:
-4 16 -64
-3 9
-27
-2 4
-8
-1 1
-1
0 0
0
1 1
1
2 4
8
3 9
27
4 16
64
Du kan lave en datafil magen til med en hvilken som helst editor. Hvis man bare beder gnuplot om at plotte filen
gnuplot> plot 'testdata'
fåes et plot med ni prikker svarende til kolonne to plottet mod kolonne et. Man kan også få plottet linier mellem punkterne
gnuplot> plot 'testdata' with lines
eller få plottet både punkter og linier
gnuplot> plot 'testdata' with linespoints
Men hvad så med tallene i den tredie kolonne? De kan plottes med følgende kommando:
gnuplot> plot 'testdata' using 1:3 with linespoints
Det ses at "plot 'testdata'" og "plot 'testdata' using 1:2" er ækvivalente kommandoer. Man angiver hvilket udsnit af plottet man vil se med kantede parenteser, på samme måde som når man plotter funktioner. Man kan lave flere plot i den samme graf:
gnuplot> plot 'testdata' with linespoints, 'testdata' using 1:3 with linespoints
Nu begynder kommandoliniens længde at blive et problem. Et nyttigt trick er at man med '' kan angive "den samme datafil igen". Når dette kombineres med forkortelseslisten nederst på denne side kan kommandoen skrives meget kortere:
gnuplot> p 'testdata' w lp,'' u 1:3 w lp
Funktionsplot og plot af data fra datafiler kan kombineres:
gnuplot> plot 'testdata', 'testdata' using 1:3, x**2, x**3
Kommandoerne "help functions" og "help operators" viser hvilke matematiske funktioner og operatorer der er til rådighed i gnuplot, og beskriver hvordan de bruges.
gnuplot> f(x) = x**a
For at tjekke at tingene virker gentager vi plottene fra før:
gnuplot> a = 2.0
gnuplot> plot 'testdata',f(x)
gnuplot> a = 3.0
gnuplot> plot 'testdata' using 1:3,f(x)
Vi kan fitte os frem til a's værdi med gnuplots fittekommando:
gnuplot> fit f(x) 'testdata' via a
Herefter er det en god ide at plotte funktionen sammen med datapunkterne for at se om fittet ser rimeligt ud:
gnuplot> plot 'testdata',f(x)
Fittet giver a = 2 fordi vi fittede til tallene i datafilen med x-værdierne i kolonne et og y-værdierne i kolonne to. Dette er underforstået når man ikke angiver hvilke kolonner der skal bruges, præcis på samme måde som med "plot"-kommandoen. Hvis man vil fitte med kolonne tre som y-værdier hedder kommandoen:
gnuplot> fit f(x) 'testdata' using 1:3 via a
Den giver det overraskende og forkerte resultat a = 1 ! Et plot af funktionen og datapunkterne viser da også at fittet er håbløst
gnuplot> plot 'testdata' using 1:3, f(x)
Hvad gik der galt? Jo, fittefunktionen finder et parametersæt, der giver et lokalt minimum for afvigelsen mellem funktionen og datapunkterne. Der er absolut ingen garanti for, at det er et globalt minimum, og der er heller ingen garanti for, at det fitter særlig godt. Det gælder derfor om at give et godt startgæt for ens parametre, således at fittefunktionen finder frem til et relevant minimum:
gnuplot> a = 2.5
gnuplot> fit f(x) 'testdata' using
1:3 via a
gnuplot> plot 'testdata' using 1:3,
f(x)
Hvis man har data fra den virkelige verden, kan det være svært at afgøre, om et fit er godt eller skidt, og specielt om nu et bestemt fit er bedre eller værre end et andet. Fittefunktionens output fortæller dig noget om hvor godt eller skidt fittet er. Prøv at køre fittet igen. Tallet ud for "final sum of squares of residuals" er et mål for, hvor tæt den fittede funktion ligger på de data, der blev fittet til. (Det er kvadratet på afvigelsen mellem den fittede funktion og det enkelte datapunkt, summeret over alle datapunkter. Mere præcist er det summen over alle datapunkter, i, af (yi-f(xi))2.) Et perfekt fit har værdien 0, et dårligt fit har en høj værdi. Hvis du sammenligner de to fit til tredie kolonne i "testdata" (med startgættene a=2.0 og a= 2.5), skulle dette være meget tydeligt. Fittefunktionen giver også et andet mål for hvor godt fittet er i form af usikkerheder på de fittede parametre. Lav usikkerhed svarer selvsagt til et bedre fit end en høj usikkerhed. Disse usikkerheder kan ikke beregnes i eksemplet her, fordi fittet passer perfekt. Med data fra den virkelige verden sker den slags ikke! Der er meget mere at sige om datafitning, usikkerheder på parametre og brugbarheden af det resultat, man kommer frem til. Nogle basale overvejelser findes her. Hvis du vil vide mere, så læs
gnuplot> print a
A -> B
Hvis reaktionen forløber efter massevirkningskinetik er reaktionshastigheden givet ved v = k[A]. Man kan derfor opstille en differentialligning, der beskriver hvordan koncentrationen af A ændrer sig med tiden
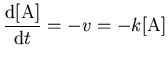
og denne differentialligning kan løses ved separation af de variable [A] og t:
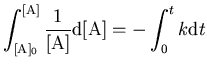
hvilket giver løsningen
[A](t) = [A]0e-kt
hvor [A]0 er startkoncentrationen af A. Et udtryk for [B](t) kan udledes på samme måde, og man får [B](t) = [B]0ekt. Fortegnsskiftet på kt skyldes at d[B]/dt = v = -d[A]/dt.
I filen eksempel.dat er der et datasæt fra en simulering af reaktionen A -> B. Gem filen på harddisken og start gnuplot. [A] plottes nu som funktion af tiden med følgende kommando:
gnuplot> plot 'eksempel.dat' with lines
Vi kan fitte udtrykket for [A](t) til datasættet for at bestemme de værdier af [A]0 og k der blev brugt i simuleringen. Først defineres en funktion så den beskriver As tidsudvikling [A](t):
gnuplot> f(x) = a0*exp(-k*x)
(Læg mærke til at der skal bruges 'x' i definitionen af f(x). Gnuplot forstår ikke udtrykket hvis man bruger 't').
Herefter skal man give nogle rimelige startgæt for de to parametre [A]0 og k. Når man plotter datasættet ser man at et godt startgæt for [A]0 er [A]0 = 10. For k er det tilstrækkeligt at angive at k > 0, så man kan f.eks. give følgende startgæt til gnuplots fittefunktion
gnuplot> a0 = 10.0
gnuplot> k = 1.0
og derefter lave fittet:
gnuplot> fit f(x) 'eksempel.dat' via a0, k
Som det ses er usikkerhederne på fittet af de to parametre små, og et plot af det fittede udtryk sammen med datapunkterne viser også at fittet er godt:
gnuplot> plot 'eksempel.dat', f(x)
De fittede værdier [A]0 = 12.0 og k = 0.1 er
da også præcis de værdier der blev brugt i simuleringen
af reaktionssystemet A -> B.
gnuplot> set terminal postscript
og dirigere gnuplots output ned i en bestemt fil (her "plot.ps") med kommandoen
gnuplot> set output 'plot.ps'
Alt hvad man herefter plotter bliver skrevet ned i den angivne fil i postscriptformat. Filen udskrives med shell-kommandoen "lpr". Bemærk at I skal udskrive på den printer i A109, der har navnet "aps". Printkommandoen bliver derfor "lpr -Paps <filnavn>".
Når man er færdig med at skrive ned i postscriptfilen, vender man tilbage til gnuplots normale output til skærmen med kommandoen
gnuplot> set terminal x11
gnuplot> set terminal postscript
gnuplot> set output 'plot.ps'
gnuplot> replot
gnuplot> quit
> lpr -Paps plot.ps
Kommandoen "replot" gentager det seneste plot, så der rent faktisk kommer noget ned i filen "plot.ps". Man kan selvfølgelig også skrive en normal plottekommando i stedet for at bruge "replot"-kommandoen.
I eksemplet ovenfor ender man med at forlade gnuplot for at udskrive. Det er både upraktisk og unødvendigt. I stedet for kan man skrive:
gnuplot> set terminal postscript
gnuplot> set output 'plot.ps'
gnuplot> replot
gnuplot> ! lpr -Paps plot.ps
gnuplot> set terminal x11
Her udnyttes at man med udråbstegnet kan udføre shell-kommandoer inde fra gnuplot. Nedenfor findes flere nyttige tricks, som gør gnuplot mere praktisk.
gnuplot> help
Man får en bestemt kommandos hjælpeside ved at skrive kommandoens navn efter spørgsmålstegnet. For eksempel får man hjælp til fittefunktionen ved at skrive
gnuplot> help fit
gnuplot> !ls
mens kommandoen
gnuplot> !xterm &
skaffer en en ny terminal, uden at man behøver at forlade gnuplot.
Fittefunktionens output kan også nemt ses:
gnuplot> !less fit.log
set samples 10000 # udregn flere
punkter for at undgå hakkede plots
a=1.0
# karakteristisk tid for amplitudens henfald
b=25.0
# svingningens frekvens
plot [0:2*pi] exp(-a*x)*sin(b*x)
vil gnuplotkommandoen
gnuplot> load 'sinus.gnu'
plotte en dæmpet svingning. (Brug f.eks. emacs til at skrive tekstfilen.)
To kommandoer, der er meget nyttige sammen med kommandofiler, er call og replot. call er en avanceret udgave af load, der gør det muligt at kalde en kommandofil med parametre. Se gnuplots hjælpesider for detaljer. Når man kalder replot gentages den sidst udførte plottekommando simpelthen. Dette kan eksempelvis udnyttes til nemt at få en graf udskrevet på printeren:
# kommandofil til udskrift af den sidst plottede graf
set terminal postscript # generer postscript
output
set output 'xxx.ps' #
skriv i filen xxx.ps
replot
# gentag det sidste plot
!lpr -Paps xxx.ps
# send postscriptfilen til printeren
set terminal x11
# skriv til skærmen på normal vis igen
gnuplot> plot 'datafil' index 1 using 1:3 with lines
Første blok har index 0, anden blok har index 1 osv. Nøgleordet "index" kan både bruges med plottefunktionen og med fittefunktionen. I begge tilfælde skal det angives lige efter filnavnet for at virke.
help
?
index
i
output
o
plot
p
quit
q
terminal
term
title
tit
using
u
with lines
w l
with linespoints w lp